EHSAN KHATAMI

My Research

My research interests in condensed matter physics lie mostly in the fields of strongly correlated electronic systems (the Hubbard models, their numerical or perturbative solutions, high-temperature superconductivity, ...), frustrated magnetism (quantum spin liquids and phase transitions, thermodynamics, ...), quantum non-equilibrium dynamics of isolated many-body systems, and unltracold gases in optical lattices. A significant part of my research is the development and implementation of various numerical techniques, such as quantum Monte Carlo, exact diagonalization, dynamical mean field theory, and linked-cluster expansions, to solve theoretical models, believed to describe real materials to varying extent.

Schematic phase diagram of the square lattice Hubbard model, with next-nearest-neighbor hopping, obtained using DCA. For more info, see this.

My thesis research was on superconducting properties and quantum critical behavior of the two-dimensional Hubbard model with parameters believed to be appropriate for cuprate superconductors, including a nonzero next nearest-neighbor hopping amplitude on the square lattice, which allowed us to study the possible role of phase separation in the superconducting transition of this model. For that, we mostly used the dynamical cluster approximation (DCA), one of the cluster extensions of the dynamical mean field theory, and exact diagonalization. An important tool in these studies was the method I developed in which the determinantal quantum Monte Carlo is employed as a fast cluster solver for the DCA.

Entropy of the checkerboard lattice Heisenberg model develops a peak at the maximally frustrated point by lowering temperature. For more info, see this.

More recently, my studies of frustrated magnets, as well as itinerant electron models, also involve a novel computational technique for quantum lattice models, namely, the numerical linked-cluster expansions (NLCEs). Within NLCEs, temperature-dependent properties in the thermodynamic limit can be obtained from exact diagonalization of small clusters. After writing my own NLCE codes from scratch for a number of expansion schemes and lattice geometries, my collaborators and I have been studying the thermodynamic properties and phase transitions of several frustrated magnetic systems, such as the antiferromagnetic Heisenberg model on the checkerboard and kagome lattices and models describing the clinoatacamites. We have also employed NLCEs to study thermodynamics of strongly-interacting fermions in two-dimensional optical lattices with square and honeycomb geometries.

Left: isentropic curves of the system of strongly-interacting fermions in a 2D optical lattice in the temperature-characteristic density space as calculated exactly using NLCE. Right: profiles of density (top), and nearest-neighbor spin correlations (bottom) at the specific points indicated in the left panel. For more info, see this.

.

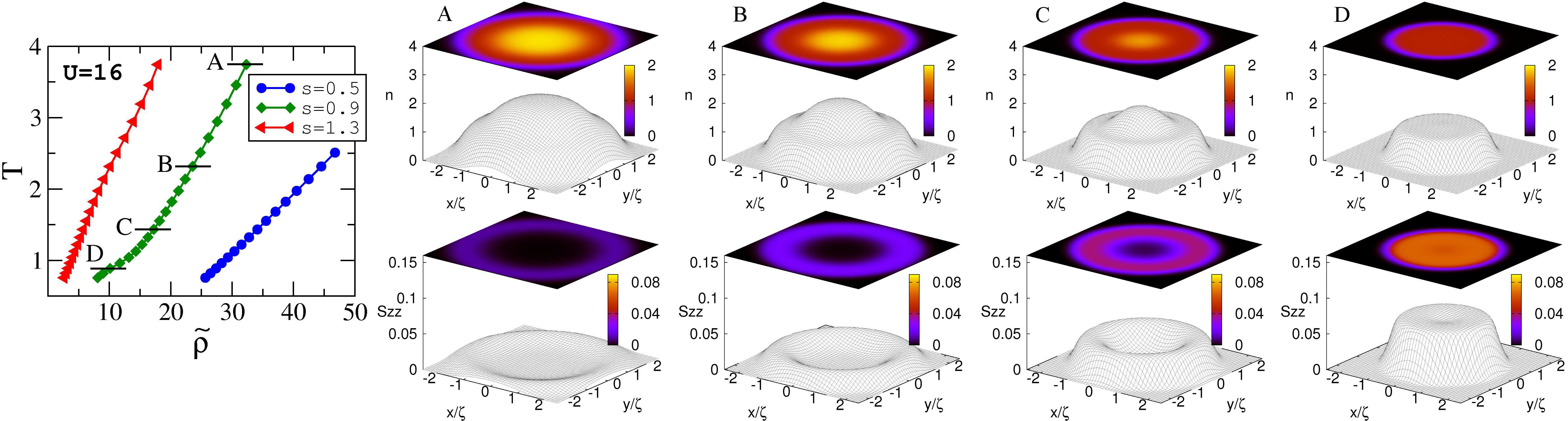
Power law relaxation of observables after a quench to their thermal expectation values in a disordered system. For more info, see this.

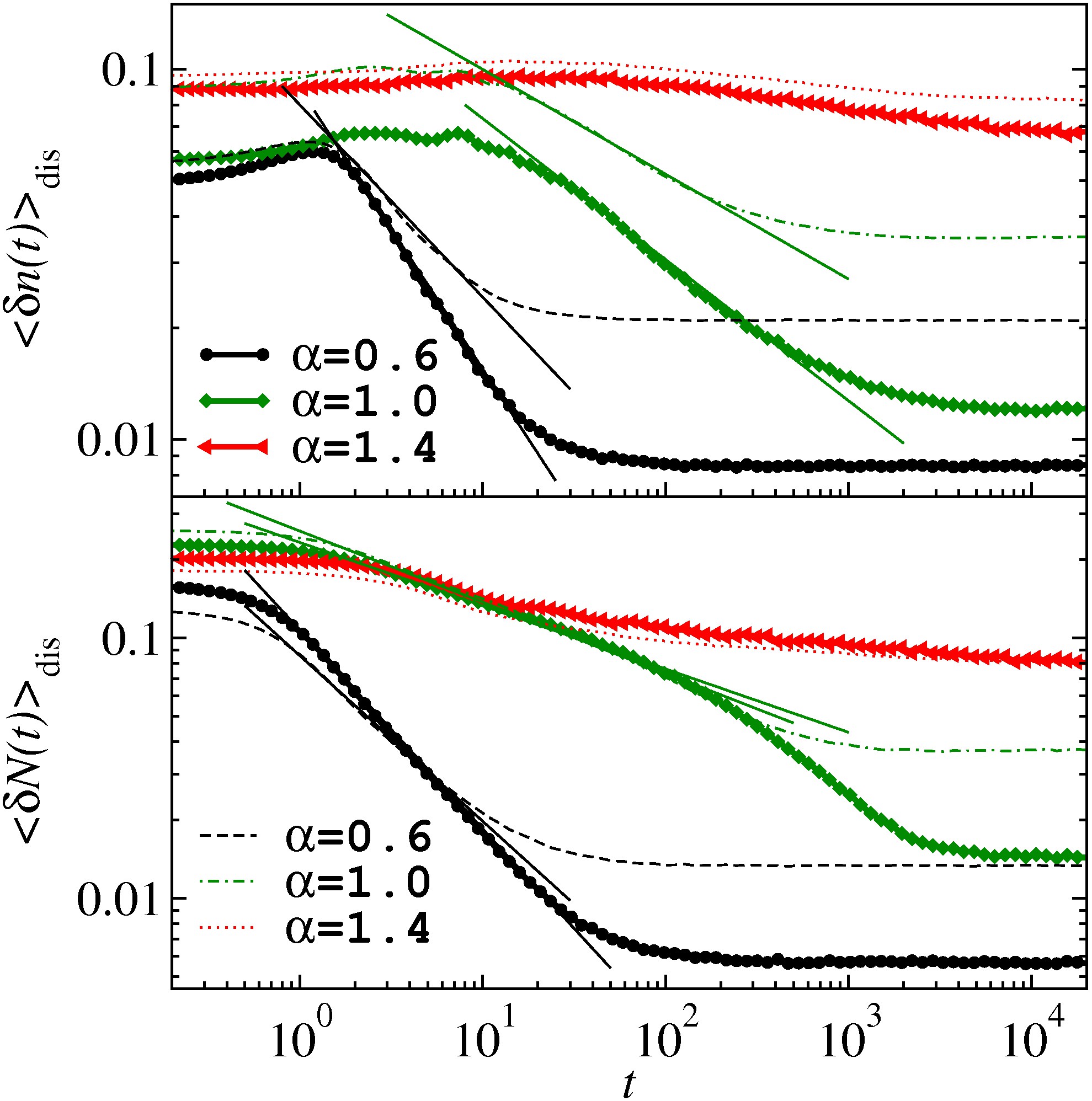I am also interested in dynamics and description after relaxation of isolated quantum systems taken out of equilibrium. In one study, I explored properties of a one-dimensional system of spinless fermions with short-range interactions and long-range random hopping after a quantum quench i.e., sudden change of the disorder realization. We found that, many-body localization effects in this model prevent thermalization even if the classical motion is chaotic. We also found a new route towards thermal equilibrium in the delocalized regime, which is characterized by a power-law, as opposed to exponential, approach to thermal expectation values, and thus, the lack of a typical relaxation time.

Histograms of the differences of the fluctuation and dissipation correlation functions over time after the quench. Results are plotted for two different system sizes and, from top to bottom, for a quench from integrable to integrable, nonintegrable to integrable, and integrable to integrable systems, respectively. For more info, see this.

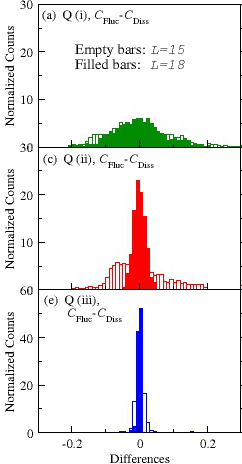
In another recent study, I have examined the validity of the fluctuation-dissipation theorem for out-of-equilibrium quantum systems. We focused on the dynamics of trapped hard-core bosons in one-dimensional lattices with dipolar interactions, in which the strength of the interaction is changed during the quench. We found that integrability of the system (having as many integrals of motion as the degrees of freedom) plays a crucial role in the validity of the theorem. Namely, the theorem holds if the system is nonintegrable after the quench. Interestingly, it also holds if the system is integrable provided that the initial state is an equilibrium state of a nonintegrable Hamiltonian.

During my current collaboration with Prof. Sriram Shastry and his group at the University of California, Santa Cruz, I have implemented highly efficient strong-coupling expansions to obtain the Green's function and other correlation functions of the infinite-U Hubbard model using many of the tools I had learned from the NLCEs. I have also learned about the extremely-correlated Fermi liquid (ECFL) theory, recently introduced by Prof. Shastry. These expansions have provided very useful tools for the study of the electronic spectral properties of this model and, for the first time, benchmarking of the ECFL solutions against exact results in the appropriate parameter region. We are currently working on the efficient calculation of dynamic density-density and spin-spin correlators to be able to better characterize the state of the system.

Last updated November, 2013